Langkah Menguasai Binary Search Tree: Panduan Praktis untuk Programmer

1. Apa itu Binary Search Tree (BST)?

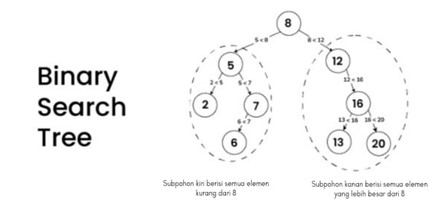
Binary Search Tree (BST) atau Pohon Pencarian Biner adalah struktur data non-linear yang tersusun atas node-node (simpul) yang saling terhubung. Setiap node memiliki nilai (key) dan dapat memiliki dua buah child node (anak), yaitu node kiri dan node kanan. Properti ini disebut properti BST dan memungkinkan pencarian, penyisipan, dan penghapusan elemen di pohon secara efisien.

2. Properti dalam Binary Search Tree (BST)

Dalam Binary Search Tree terdapat beberapa property yang digunakan, yaitu

1. Subpohon kiri node hanya berisi node dengan kunci lebih rendah dari kunci node.

2. Subtree kanan node hanya berisi node dengan kunci lebih besar dari kunci node.

3. Ini berarti segala sesuatu di sebelah kiri akar kurang dari nilai akar dan segala sesuatu di sebelah kanan akar lebih besar dari nilai akar. Karena kinerja ini, pencarian biner sangat mudah. 4. Subpohon kiri dan kanan masing-masing juga harus menjadi pohon pencarian biner.

5. Tidak boleh ada node duplikat (BST mungkin memiliki nilai duplikat dengan pendekatan penanganan yang berbeda)

3. Operasi Dasar pada Binary Search Tree (BST)

3.1 Mencari Node dalam BST

Mencari di BST berarti menemukan node tertentu dalam struktur data. Dalam pohon pencarian Biner, mencari node itu mudah karena urutannya spesifik. Langkah-langkah mencari node di pohon Pencarian Biner terdaftar sebagai berikut.

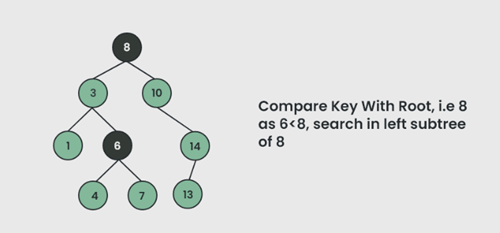
a. Pertama, bandingkan elemen yang akan dicari dengan elemen akar pohon.

-Jika root cocok dengan elemen target, maka kembalikan lokasi node.

- Jika tidak cocok, maka periksa apakah item tersebut kurang dari elemen root, jika lebih kecil dari elemen root, maka pindah ke subpohon kiri.

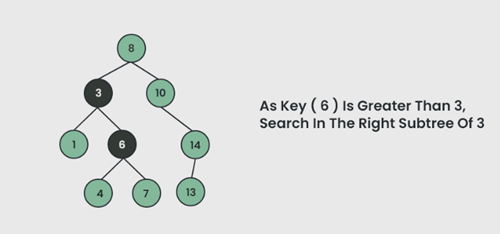
- Jika lebih besar dari elemen root, maka pindah ke subpohon kanan.

b. Ulangi prosedur di atas secara rekursif sampai kecocokan ditemukan.

c. Jika elemen tidak ditemukan atau tidak ada di pohon, kembalikan NULL.

Ø  Sekarang, mari kita pahami pencarian di pohon biner menggunakan contoh:

Di bawah ini diberi BST dan kita harus mencari elemen 6.

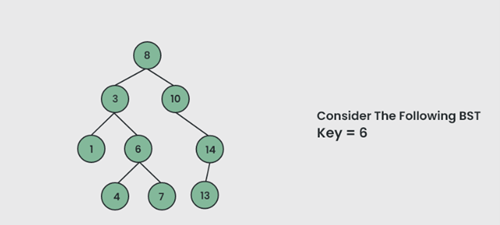
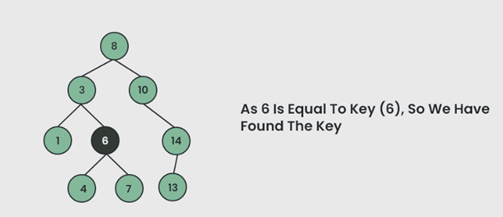
Program untuk mengimplementasikan pencarian di BST :

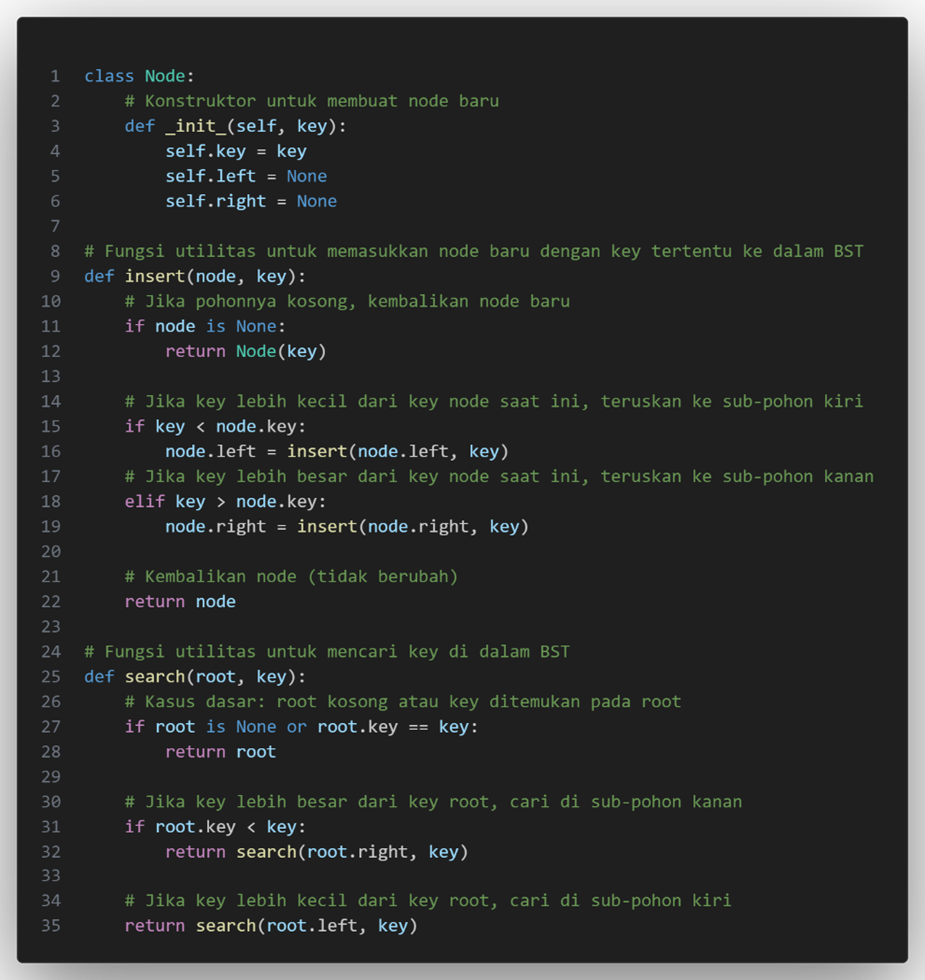
3.2 Masukkan Node ke Binary Search Tree (BST)

Kunci baru selalu disisipkan pada daun. Mulailah mencari kunci dari akar hingga simpul daun. Setelah simpul daun ditemukan, simpul baru ditambahkan sebagai anak dari simpul daun.

Perhatikan BST Berikut :

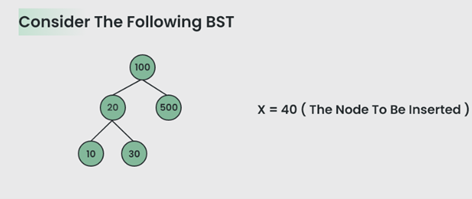
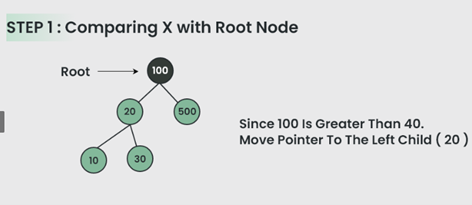
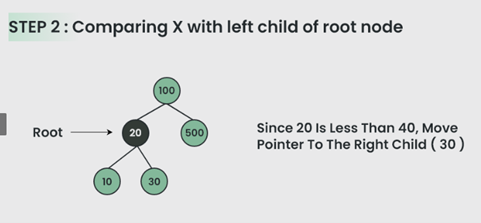
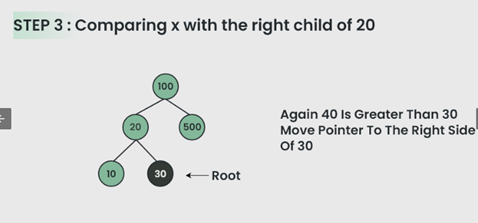
Program untuk Memasukkan Node ke Binary Search Tree

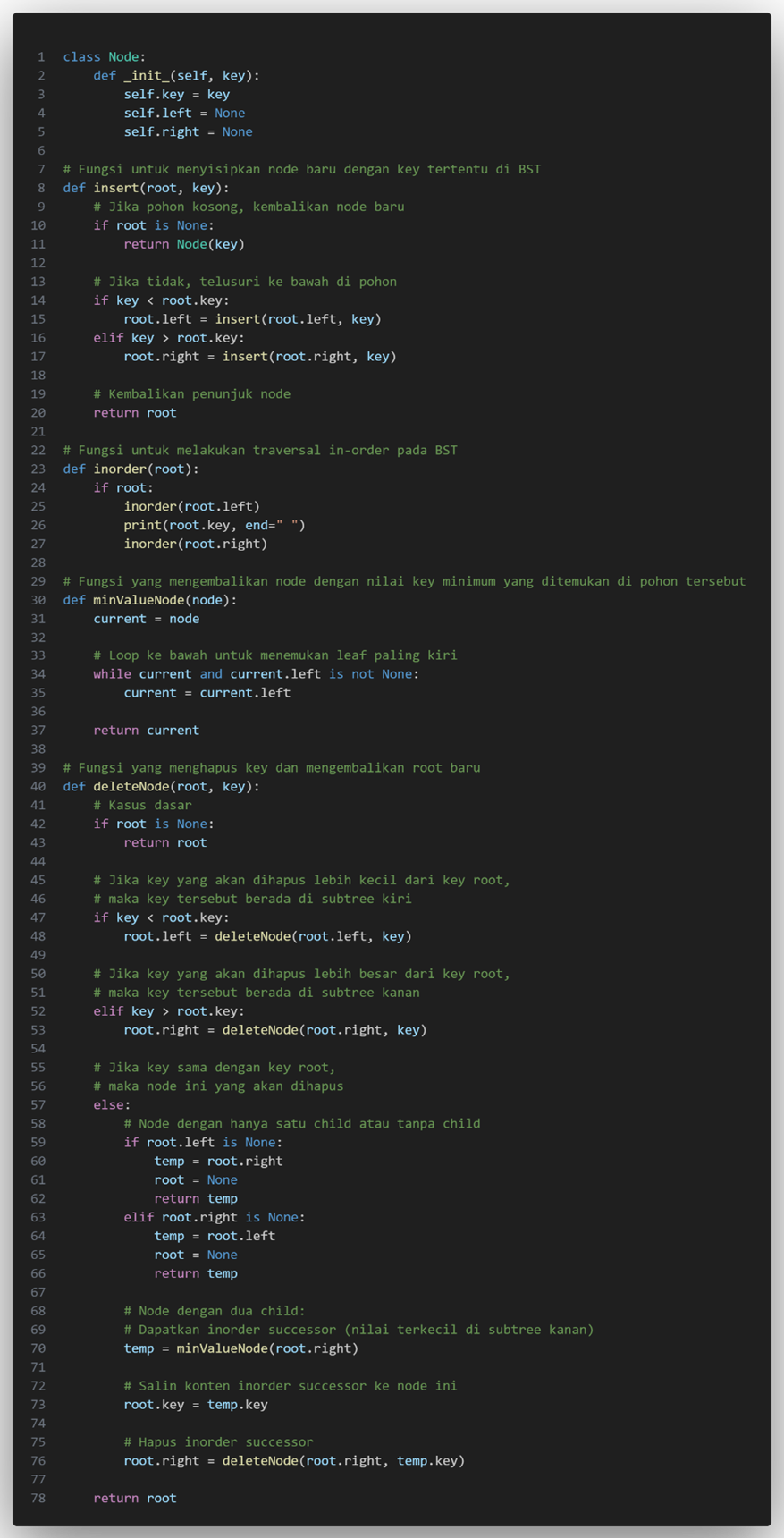
3. 3 Hapus Node BST :

Ini digunakan untuk menghapus node dengan kunci tertentu dari BST dan mengembalikan BST baru.Skenario berbeda untuk menghapus node: Node yang akan dihapus adalah node daun : Sederhana saja, Anda bisa membatalkannya.

Kasus 1 : Hapus Node Daun di BST

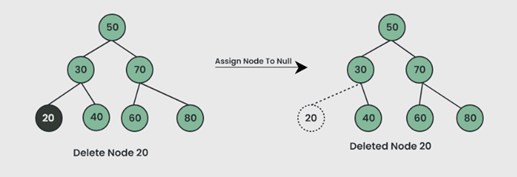
Kasus 2 : Hapus Node dengan anak Tunggal di BST 

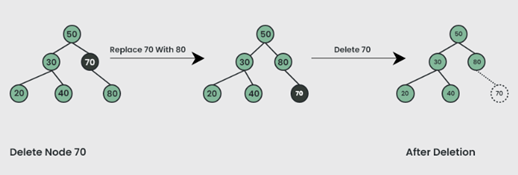
Kasus 3 : Hapus Node dengan kedua anak di BST

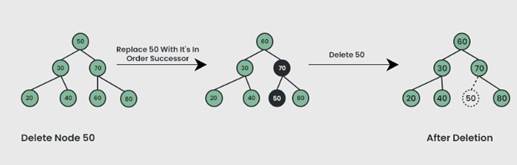
Jaga hal-hal berikut saat menghapus node BST:

1. Perlu mencari tahu apa yang akan menjadi pengganti node yang akan dihapus.

2. Ingin meminimalkan gangguan pada struktur pohon yang ada

3.Dapat mengambil node pengganti dari node yang dihapus di subpohon kiri atau kanan.

4. Jika mengambil if dari subpohon kiri, kita harus mengambil nilai terbesar pada subpohon kiri.

5. Jika mengambil if dari subpohon kanan, kita harus mengambil nilai terkecil pada subpohon kanan.

Program untuk hapus Node BST :

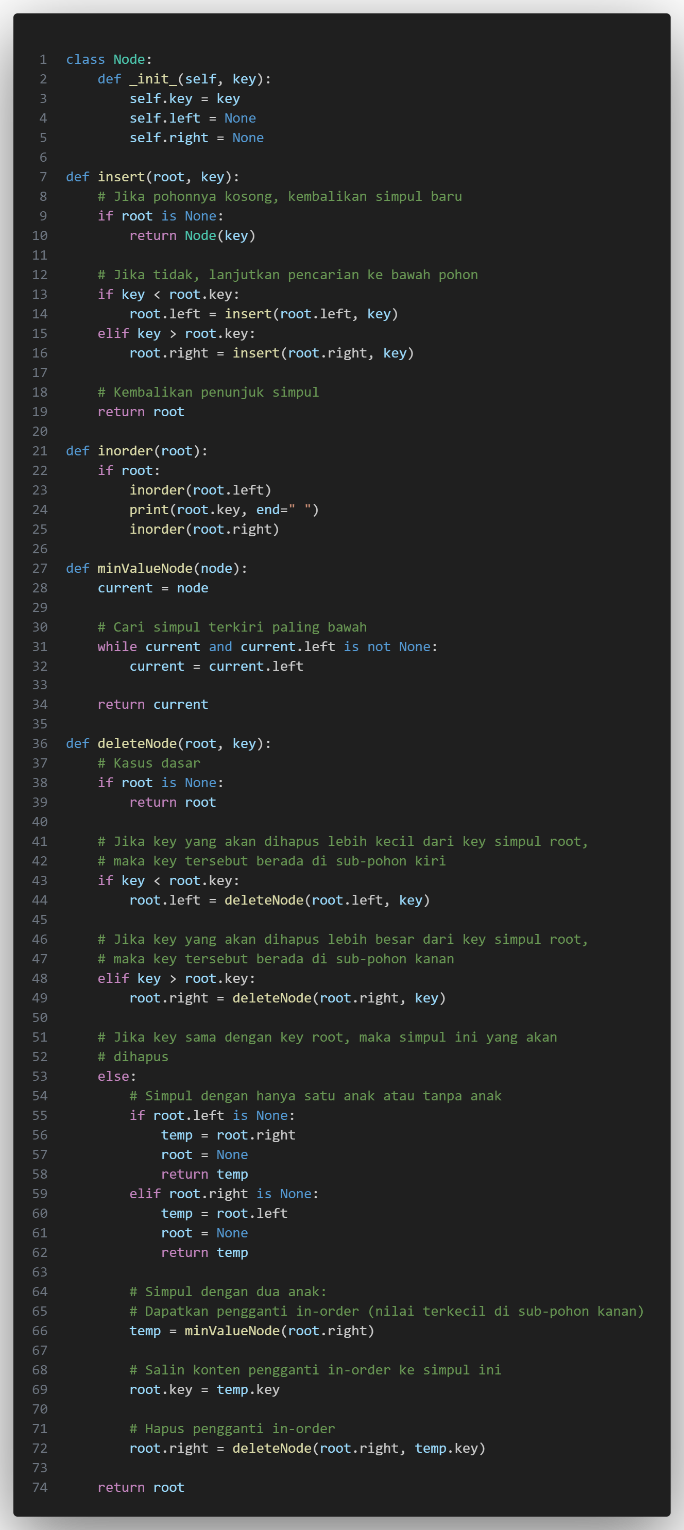
4. Traversal (Inorder traversal BST) :

Dalam kasus pohon pencarian biner (BST), traversal Inorder memberikan node dalam urutan yang tidak menurun. Kita mengunjungi anak kiri terlebih dahulu, lalu akar, dan kemudian anak kanan.

Berikut implementasi cara melakukan inorder traversal pada Binary Search Tree:

Program untuk Inorder Traversal BST :

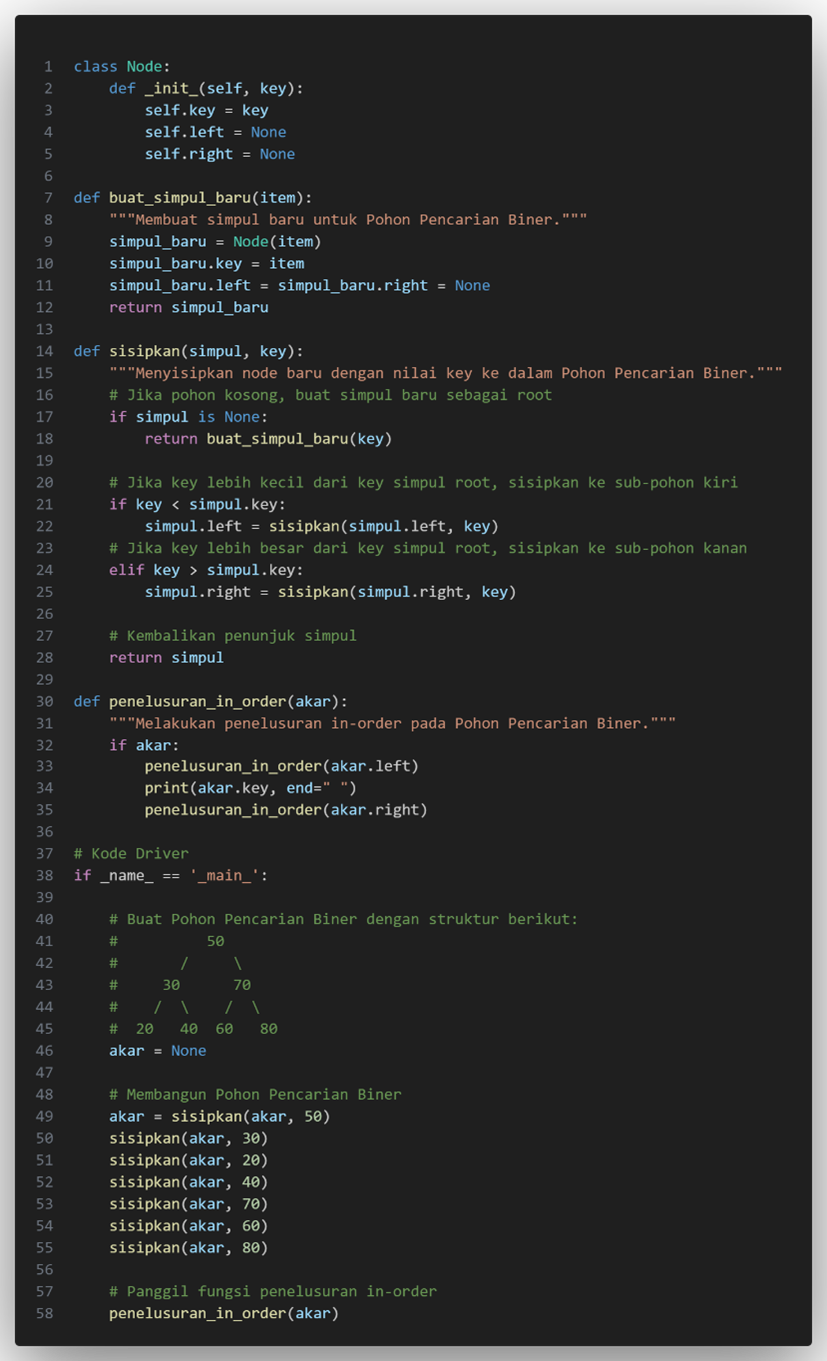
5. Penerapan BST:

1. Algoritme grafik: BST dapat digunakan untuk mengimplementasikan algoritma grafik, seperti pada algoritma pohon merentang minimum.

2. Antrian Prioritas: BST dapat digunakan untuk mengimplementasikan antrian prioritas, dimana elemen dengan prioritas tertinggi berada di akar pohon, dan elemen dengan prioritas lebih rendah disimpan di sub pohon.

3. Pohon pencarian biner yang menyeimbangkan diri: BST dapat digunakan sebagai struktur data yang menyeimbangkan diri seperti pohon AVL dan pohon Merah-hitam.

4. Penyimpanan dan pengambilan data: BST dapat digunakan untuk menyimpan dan mengambil data dengan cepat, seperti di database, dimana pencarian catatan tertentu dapat dilakukan dalam waktu logaritmik.

6. Keuntungan:

1. Pencarian cepat: Pencarian nilai tertentu dalam BST memiliki kompleksitas waktu rata-rata O(log n), dimana n adalah jumlah node dalam pohon. Ini jauh lebih cepat daripada mencari elemen dalam array atau daftar tertaut, yang memiliki kompleksitas waktu O(n) dalam kasus terburuk.

2. Penjelajahan dalam urutan: BST dapat dilintasi secara berurutan, yang mengunjungi subpohon kiri, akar, dan subpohon kanan. Ini dapat digunakan untuk mengurutkan kumpulan data.

3. Hemat ruang: BST hemat ruang karena tidak menyimpan informasi yang berlebihan, tidak seperti array dan daftar tertaut.

7.Kekurangan:

1. Pohon miring: Jika pohon menjadi miring, kompleksitas waktu operasi pencarian, penyisipan, dan penghapusan akan menjadi O(n) dan bukan O(log n), yang dapat membuat pohon menjadi tidakefisien.

2. Waktu tambahan yang diperlukan: Pohon yang menyeimbangkan diri memerlukan waktu tambahan untuk menjaga keseimbangan selama operasi penyisipan dan penghapusan.

3. Efisiensi: BST tidak efisien untuk kumpulan data dengan banyak duplikat karena akan membuang-buang ruang.

Author : Yoga Ari Anggoro | 23091397049